الذكاء الإصطناعي : البحث و إستراتيجيات التحكم (1) #الدرس الثلاثون

الجزئ الأول من الدرس الثلاثون في الذكاء الإصطناعي : البحث و إستراتيجيات التحكم (1) ...

البحث و إستراتيجيات التحكم Search and Control Strategies :

تعود الكلمة "بحث" إلى البحث عن حلول في فضاء المسألة، يُسيِرُ البحث مختلف أنواع إستيرتيجيات أنواع التحكم بالبحث، و تعرف الإستيراتيجية بواسطة لأخذ الترتيب الذي يتم فيه الوصول إلى النقطة في فضاء المسألة؛ و نُقيِم إستراتيجيات التحكم في الأبعاد التالية : التمام Completeness و تعقيد الوقت "أي الكلفة الزمنية" Time Complexity و تعقيد فضاء المعرفة و أمثلية الحل Optimality، و فيما يلي سنوضح بعض المصطلحات للبحث المهم، و من ثم سنشرح خوارزميات البحث و إستيراتيجياتها ...

1. البحث Search :

البحث هو إختيار نظامي لمجموعة حالات من أجل معرفة المسار من الحالة الإبتدائية إلى حالة الهدف، البحث عادةً ينتج من نقص المعرفة Lack of Knowedge، و يكتشف البحث البدائل المعرفية للوصول إلى الإجابة الأفضل، مخرجات خوارزمية البحث هو إجابة تعرض كمسار من الحالة الإبتدائية مع الحالة التي تتطاfق مع حالة الهدف؛ و البحث Search هو منهجية متعبة لأجل حل مسار عامة الغرض General Purpose : يعمل لإيجاد النقاط التي لها خصائص معينة في الشجرة البيانية التي تمثل فضاء البحث، و تقوم طرق البحث باستكشاف فضاء البحث Search Space بشكل ذكي "intelligently"، و تقييم الخيارات الممكنة بدون التحقق من أي خيار فردي.

2. شجرة البحث Search Tree :

شجرات البحث هي عبارة عن فهارس متعددة المستويات مستخدمة لقيادة البحث عن عناصر البيانات وفق بعض معايير البحث المعطاة؛ أنظر إلى الصورة :




يبدأ البحث عند الجذر Root و يستكشف النقاط Nodes للبحث عن النقطة الهدف التي تحقق الظروف أو الشروط التي تعتمد عليها المسألة، و من أجل بعض المسائل قد تكون أي نقطة مقبولة للحل، مثلاً النقطتين N و J في المثال رالمقابل، و في بعض المسائل تكون النقطة J هي الأكثر قبولاً للحل لأنها في المستوى الأقرب للنقطة الجذر.

خوارزميات البحث Search Algorithms :

كثيرٌ من خوارزميات البحث التقليدية تُستخدمُ في الذكاء الإصطناعي، و للمسائل المعقدة لا تستطيع الخوارزميات التقليدية إيجاد الجواب ضمن بعض حدود الفضاء و الزمن الفعلي، و بناء على ذلك؛ فقد تم تطوير كثيرٌ من التقنيات الخاصة باستخدام دوال الكشف Heuristic Function، و الخوارزميات التي تستخدم دوال الكشف تسمى خوارزميات الكشف، و خوارزميات الكشف ليست ذكية حقاً؛ هي فقط تبدو و كأنها ذكية، لأنها بإختصار تقدم آداءاً أفضل، و خوارزميات الكشف أيضاً أكثر كفاءة، لأنها تأخذ مميزات التغذية الراجعة FeedBack من البيانات لتوجيه مسار البحث.

• خوارزميات البحث الغير الموجه Uninformed أو خوارزميات بحث القوة "العمياء"، من خلال فضاء البحث، يتم فحص كل الخيارات الممكنة للحل ما إذا كان أي خيار يطابق ما تتطلبه المسألة.
• خوارزميات البحث الموجهة Informed Search تستخدم هذه الخوارزميات دوال الكشف، هذه الدوال تكون مخصصة حسب المسألة، و يتم تطبيقها للسير بالبحث من خلال فضاء البحث، و ذلك محاولة لتقليل كمية الزمن الذي يستغرقه البحث.

آلية الكشف الجيدة تستطيع آداء بحث في أي لحظة متجاوزة أي بحث غير موجه، و مسألة البائع الجوال TSP مثال على ذلك، حيث يكون الهدف إكتشاف الحل الجيد بدلاً من إكتشاف الحل الأفضل؛ في المسائل المشابهة لمسألة البائع المتجود (TSP)، يستمر البحث باستخدام المعلومات الحالية حول المسألة للتنبؤ حول المسار، الذي يكون أقرب إلى الهدف و يتبع له، مع أنه لا يمكن أن نضمن دائماً إكتشاف الحل الممكن الأفضل، هذه التقنيات تساعد في إكتشاف الحل من خلال زمن و فضاء معقولين. و هناك عدد من خوارزميات البحث المعروفة منها :

1. بحث إفترض واختبر Generate and Test Search.
2. البحث عن الأفضل أولاً Best First Search.
3. البحث الطماع Greedy Search.
4. البحث بالشرط Constraint Search.
5. تحليل النهاية المطلوبة Means ands Analysis.
6. البحث *A* Search A.
7. و هناك العديد من الخوارزميات، سواء كانت مطورة عنها أو مركبة منها.

التمثيل الهرمي لخوارزميات البحث :

تمثيل أغلب خوارزميات البحث موضح في الشكل أدناه، و هي تبدأ بالتصنيفين الأساسين للبحث و هما البحث الموجه و غير الموجه، البحث الغير موجه يسمى أيضاً بقوة الصرفة أو الشامل أو البحث الأعمى، و فيه لا تستخدم معلومات عن المسألة لإرشاد البحث، و لذك قد لا يكون كفوؤاً. أما البحث الموجه يسمى أيضاً بالبحث مع آلية الكشف أو البحث الذكي، و فيه تستخدم معلومات مسبقة عن المسألة من أجل مساعدة البحث، عادة تخمن المسافة إلى حالة الهدف و لهذا يكون البحث كفواً، و لكنه قد لا يكون من الممكن دائماً لقصور معلومات المساعدة مثلاً.

فضاء البحث Search Space :

هو مجموعة من الحالات التي يمكن أن نتوصل لها، مشكلة ما يسمى فضاء البحث و هذا يتعلق بتطبيق بعض المؤثرات المركبة التي تعرف آلية التواصل فيما بينها؛ مثلاً : جد المسار من البداية إلى حالة الهدف، باعتبار أن الرؤوس هي المدن، و أن الحواف هي المسافات بين المدن ...

البيان المنهجي للمسألة Formal Statement :

حل المسألة هو مجموعة من العبارات التي تصف الحالات المطلوب التعبير عنها بلغة مناسبة، و إجابة عدد كبير من المسائل يمكن وصفها باكتشاف سلسلة الأفعال التي تقود من الحالة الإبتدائية إلى الحالة النهائية و هي حالة الهدف، كل واحد واحد من هذه الأفعال يغير الحالة، و فيما يلي نموذج مسألة معرفة و مرتبة بشكل جيد :

• الحالة الإبتدائية (S).
• الدوال المؤثرة Operator Function : في الحالات الإلتقائية، أو الدوال الوريثة؛ مثال : لكل حالة x تعيد لنا (s(x مجموعة من الحالات يمكننا الوصول إليها من الحالة x بفعل واحد فقط.
• فضاء البحث State Space : كل الحالات ممكنة الوصول من البداية باستخدام أي سلسة من الأفعال.
• المسار Path : سلسلة حالات من فضاء البحث.
• تكلفة المسار Path Cost : كدالة تربط بين المسار و كلفته، و تحسب تكلفة المسار الواحد بجمع الأفعال المنفذة على طول المسار.
• حالة الهدف (G).
• إختبار الهدف Gost Test : إختيار للتأكد من كون الحالة النهائية هي حالة الهدف.

الرموز الرياضية للبحث Search Notation :

يجب علينا أن نعلم أن البحث هو الإختيار النظامي للحالات، لإكتشاف المسار من البداية أو حالة الجذر على حالة الهدف، و الرموز المستخدمة لتعريف البحث هي كالتالي :

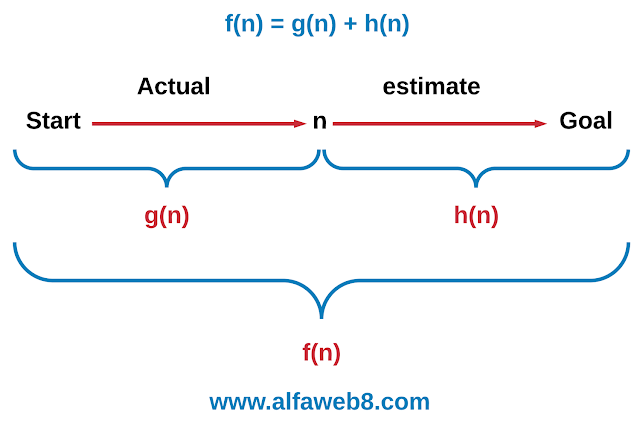
• الدالة (f(n هي دالة التقييم التي تقدر الحل الأقل تكلفة خلال النقطة n.
• الدالة (h(n هي دالة الكشف التي تقدر المسار أقل كلفة من النقطة n إلى نقطة الهدف.
• الدالة (g(n هي دالة التكلفة التي تقدر المسار أقل تكلفة من نقطة البداية إلى النقطة n.

و يعبر عن العلاقة بين هذه الوسائط الثلاثة بالقانون التالي :

إذا كانت (h(n أقل من أو تساوي التكلفة الفعلية للمسار الأقصر من النقطة n إلى الهدف، فإن قيمة (h(n غير كافية،  و القيم المقدرة لـ f و g و h يعبر عنها بالرموز ^F و ^G  و ^H على الترتيب، بحيث يكون : (F^(n)-G^(n)+H^(n ... و أجل تبسيط الكتابة هناك من يبدل الرمز ^ بالرمز * فتكون *H و هكذا.

تقدير دالة التكلفة  *Estimate Cost Function g :

عرفنا أن تقدير المسار الأقل تكلفة من نقطة البداية حتى النقطة n، و يرمز له بـ (g*(n و يعرف (g*(n بحساب تكبفة جميع المسارات من البداية حتى الحالة الحالية (الحالة التي بصددها الآن)، إذا كان فضاء البحث ممثل بشجرة؛ فتكون *g = g لأن هناك مسار واحد من نقطة البداية إلى النقطة الحالية، و لكن بشكل عام، يكون فضاء البحث بياناً Graph، أي ليس من الضرورة أن يكون شجرة؛ و إذا كان فضاء البحث بياناً فتكون *g =< g و أنه لا يمكن أن تكون *g أقل من تكلفة المسار الأمثل، فضلاً عن كونها تستطيع تجاوز التكلفة المقدرة، و يمكن أن تكون *g مساوية لـ g طبعاً في الشكل البياني Graph إن تم إختيارها بدقة أكبر.

تقدير دالة الكشف *Estimate Heuristic Function h :

نعرف أن تقدير المسار الأقل تكلفة من النقطة n إلى نقطة الهدف يرمز له بـ (h*(n، حيث أن *h هي معلومات آلية الإكتشاف تمثل التخمين أو التقدير؛ مثلاً : ما مدى صعوبة الوصول من النقطة الحالية إلى حالة الهدف ... ؟ ... يمكن تقدير قيمة *h بنقطة ما بإستخدام دالة التقييم (f(n التي تقيس جودة تلك النقطة Goodness، و يمكن لـ *h أن تأخذ قيمة مختلفة، فالقيم التي تقع بين 0 =< (h(n) >= h*(n و التي تعني خوارزمية بحث مختلفة، و إذا كانت h = *h فإننا نكون قد حصلنا على قيمة الكشف المثالية أو Perfect Heuristic، مما يعني عدم ضرورة البحث في نقاط زائدة عن الحاجة.

و سيكون الدرس القادم (الجزء الثاني من الدرس الثلاثون) عن إستراتيجيات التحكم، حيث تم تقسيم الدرس إلى جزئين لأسباب كَتجنب ملل القارئ -يتبع-